Instructor

Bell's inequality is an attempt to address the origin of the probabilistic nature in quantum mechanics, that is, is the lack of determinism a result of our lack of knowledge? The violation of it shows that "hidden instructions" of a particle do not and cannot exist. There is simply no mechanism that decides the outcome of a quantum measurement. 

Bell’s argument was first presented in 1964, as a response to a 1935 paper published by Einstein, Podolsky, and Rosen (EPR). The EPR paradox looks at entanglement between quantum particles that are very far apart. By measuring one particle, the outcome of measuring the other particle is determined instantaneously, leading Einstein to dub quantum mechanics as having “spooky action at a distance”. It was well-known at the time that the speed of light presented a fundamental speed limit in our universe, and instantaneity of measurement of entangled particles seemed to violate this rule.

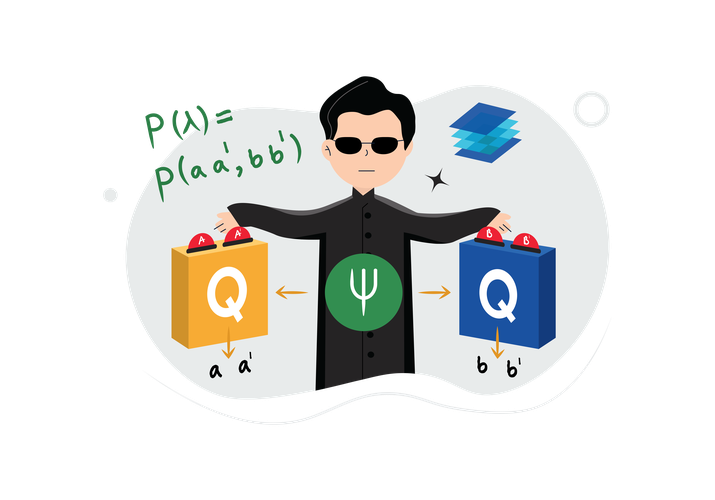
Bell made the assumption that quantum mechanics had to be “local” and particles had “hidden information”. Locality means that particles can only be affected by their neighbors, and cannot communicate faster than light. Hidden information of the particle is as described in this video by Kaszlikowski, and assumes that particles contain information needed in a deterministic universe. This is what we see in the classical world. If we toss a coin into the air, and know the force applied, the weight of the coin, air resistance, and so on, we can predict with certainty how it lands. Bell’s assumptions lead to the conclusion that the statistics of measuring an entangled pair of particles cannot exceed a particular value.

The original argument proposed by Bell included a suggestion for an experiment to verify the assumptions. However, the experiment was difficult to implement. John Clauser, Michael Horne, Abner Shimony, and Richard Holt (CHSH) proposed a different inequality, the so-called CHSH inequality, which essentially is a variant of the Bell inequality. This CHSH inequality,  presented in this video, is violated by actual experimental data in the lab. This shows us that the underlying assumptions of locality and hidden variables cannot be both true. Since we know that locality is enforced by relativity, the fact that nature does not obey Bell’s inequality then demonstrates that there are no hidden variables in quantum mechanics! Quantum objects don’t behave the same way as classical ones!

The Nobel prize in physics 2022 was awarded jointly to Alain Aspect, John F. Clauser and Anton Zeilinger for “experiments with entangled photons, establishing the violation of Bell inequalities and pioneering quantum information science”. The true nature of the smallest scales of reality are fundamentally probabilistic - no hidden information about how they behave, and with completely random outcomes when we measure them. And yet, we can make correlations between quantum objects through entanglement! 

The realization of random events at the quantum level is something that we have to learn to live with. On the other hand, the correlation between the entangled particles makes us excited to explore how we could use them in our technologies. With the strange correlations between entangled particles, we are able to perform computations that are otherwise impossible and generate secure encryption for communication.

References

Bell, J. S. (1964). On the Einstein Podolsky Rosen paradox. Physics Physique, 1(3), 195–200. https://doi.org/10.1103/physicsphysiquefizika.1.195 

Einstein, A., Podolsky, B., & Rosen, N. (1935). Can quantum-mechanical description of physical reality be considered complete? Physical Review, 47(10), 777–780. https://doi.org/10.1103/physrev.47.777 

Clauser, J. F., Horne, M. A., Shimony, A., & Holt, R. A. (1969). Proposed experiment to test local hidden-variable theories. Physical Review Letters, 23(15), 880–884. https://doi.org/10.1103/physrevlett.23.880 

The nobel prize in physics 2022. NobelPrize.org. (n.d.). Retrieved April 14, 2023, from https://www.nobelprize.org/prizes/physics/2022/press-release/ 

Nielsen, M. A., & Chuang, I. L. (2022). Quantum Computation and Quantum Information. Cambridge University Press.